물질은 상태에 따라 힘에 대해 다른 반응을 보인다.
힘을 가했을 때 원래대로 돌아가려는 성질을 탄성(elasticity)이라고 하고,
힘을 가했을 때 유체의 경우 힘에 의해서 흐르게 되는 점성(viscosity)을 가진다.
고분자의 경우 힘에 의해 변형되었다가 원래대로 돌아가려는 성질과 흐르려는 성질을 동시에 지니는데,
즉, 점탄성을 가진다는 것은 액체로서의 성질과 고체로서의 성질이 동시에 나타나는 현상이다.
시간 또는 온도에 따라서 이러한 점탄성이 변하는 정도에 따라 원하는 형태로 가공할 때에 어려움이 있을 수 있다.
따라서 이러한 성질을 잘 파악하는 것이 고분자의 가공(압출, 사출, ...)에 있어 중요하다.
* 압출(extrusion): 가래떡 뽑기
* 사출(injection): 붕어빵 찍기 (틀에 주입-inject-하는 것)
응력(Stress), 변형율(Strain), 그리고 탄성 계수(Modulus of elasticity)
- 응력(Stress)
물체에 외부에서 힘을 가하게 되면(외력), 그 힘을 상쇄하려는 내부 힘인 응력이 작용하게 된다. 따라서 물체가 힘에 의해 변형되지 않고 유지될 수 있는 것이다. (외부에서 어떤 힘든 일이 찾아오면 우리 안에 stress가 발생한다고 말하기도 하니까)
이러한 응력은 힘을 가하는 방향에 따라 인장 응력(쭈욱 잡아당길 때-고무줄 당기기), 압축 응력(인장 응력의 반대), 전단 응력(격파) 등으로 분류할 수 있다.
외력이 커지면 커질수록, 그에 반대되는 응력도 커지게 될 것이다.
- 변형율(Strain)
응력은 커지는 외력에 비례해서 커지게 되는데, 즉, 원래의 형태를 유지하려는 구간이 존재한다.
응력의 상관관계를 나타내기 위해 '얼마나 내가 변형을 시켰는지'를 정량화한 것이 변형율(strain)이다.
예를 들어, 아래 그림처럼 어떤 물체를 위아래로 쭉 잡아당길때
원래 물체가 10cm이고 내가 5cm 잡아당겼다고 하면 원래 길이 대비 5/10=0.5배 잡아당긴 것이고, 이를 변형율이라고 한다.
- 탄성 계수(Modulus of elasticity)
변형이 일어날 때, 일정 구간 동안은 원래 모양으로 복귀할 수 있는 영역, 즉 "탄성 영역(elastic region)"에 위치한다.
이때, strain과 stress가 비례하는 구간(탄성 영역)에서의 비례 상수(기울기)를 탄성계수(modulus of elasticity)라고 하며, 이렇게 쭉 늘어나게 하여 인장강도를 측정할 때의 인장 탄성 계수는 영국 학자인 토머스 영의 이름을 붙여서 Young's modulus라고 한다.
즉, 탄성계수가 클수록 잘 안늘어난다(변형하기가 어렵다)고 직관적으로 생각할 수 있다.
예를 들어, 같은 5cm (strain) 만큼 늘리는 데에 A 물질은 10 Pa (stress)가 필요하고, B 물질은 20 Pa이 필요하다면,
B의 기울기(탄성계수)가 더 크게 계산된다.
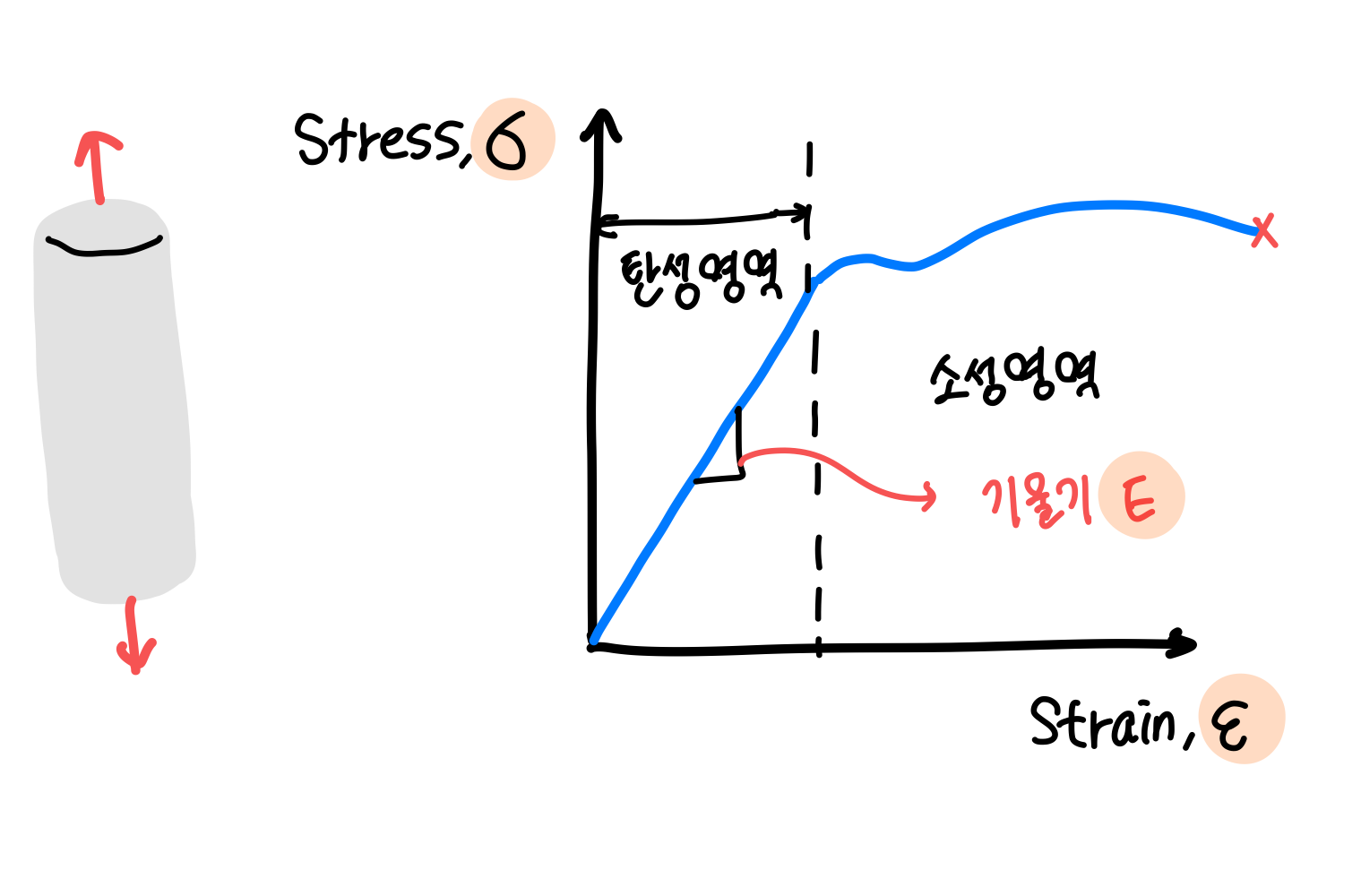
이를 지나면 더이상 원래 모양으로 돌아갈 수 없는 "소성 영역(plastic region)"에 진입하게 된다.
응력이 한없이 커질 수 있을까?
그렇지 않다. 어느 순간 물체가 깨지거나 부러지거나 등등 견디지 못하게 되는 지점(파단)이 올 것이다.
저장탄성률(Storage modulus, G'), 손실탄성률(Loss modulus, G'')
위의 예시는 탄성을 가지는 물체에 대해 강직도(stiffness)를 측정할 때, 물체가 외부에서 가해지는 변형에 대해 얼마나 탄성을 유지할 수 있는지에 대해 측정하는 방법을 소개했다.
점탄성 물질의 경우, 다양한 물성을 측정하게 되는데 이러한 점탄성에 기여하는 두 가지 요소가 있다.
예를 들어, 물에 젖은 스펀지의 탄성률(complex modulus, G*)을 생각해보자.
먼저, 스펀지 자체는 탄성을 가지고 있다. 즉, 스펀지를 약간 잡았다 당기거나, 손가락으로 눌렀다 떼면 원래 모양으로 돌아온다. 이처럼 스펀지가 가지는 탄성이 G*에 기여하는 정도를 저장 탄성률(storage modulus, G')이라고 생각해 볼 수 있다. 즉, 원래 가지고 있는 탄성을 말한다. 말랑말랑한 스펀지랑 딱딱한 스펀지를 비교한다면, 딱딱한 경우에 더 G'이 더 크게 되고, 따라서 G*이 더 커지게 될 것이다.
한편, 스펀지가 물에 젖게 되면 젖기 전에 비해서 탄성률(외부의 힘에 대해 저항하는 정도)에 변화가 생길 것이다. 예를 들어, 스펀지를 물이 아닌 시럽이나 꿀에 적신다고 하면 스펀지는 훨씬 더 큰 G*를 가지게 될 것이다. 이처럼 물은 탄성을 가지지는 않지만(=점성을 가지지만) 역시나 G*에 기여한다. 따라서, 이러한 점성이 G*에 기여하는 정도를 손실 탄성률(loss modulus, G'')이라고 한다. 손실이라고 하는 이유는, 탄성을 기준으로 하면 점성은 탄성을 잃어버린 상태이기 때문이다.
- 동적 기계 분석(dynamic mechanical analysis, DMA)
점탄성 물질의 탄성을 나타내는 G'과 점성을 나타내는 G'' 을 통해 고체에 가까운 성질을 나타내는지, 액체에 가까운 성질을 나타내는지 알 수 있다. G'와 G''이 G*에 기여하는 정도는 물질마다 다를 것이고, 단순한 합이 아닌 아래 그림과 같이 벡터 합으로 구할 수 있다.
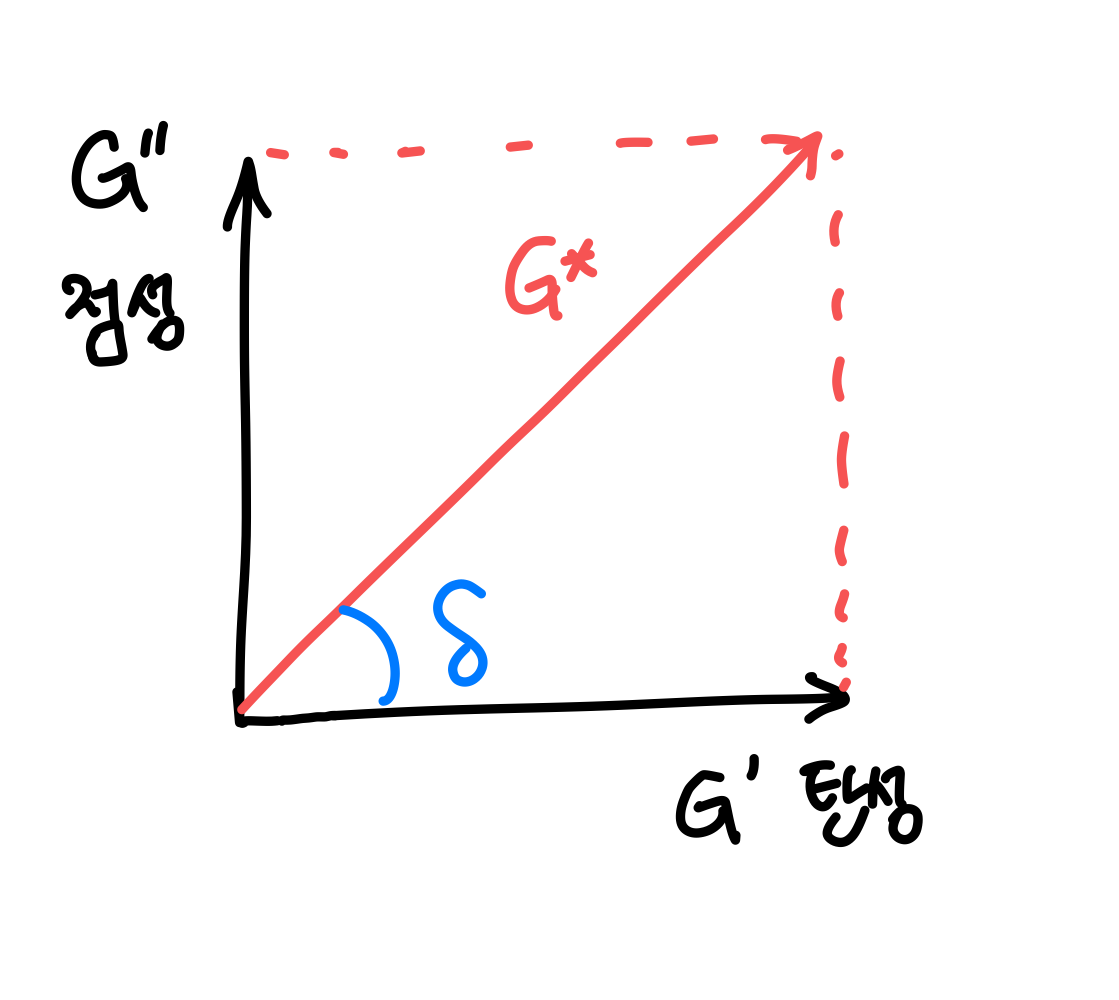
여기서 δ는 phase angle(위상 차)인데, 여러가지 측정 방법 중 널리 사용되는 동적 기계 분석(dynamic mechanical analysis, DMA)에서 알아 볼 수 있다. 점탄성은 재료의 온도를 변화시키거나 또는 주파수를 변화시켜서 측정할 수 있다.
이를 간단히 설명하면, 재료에 사인곡선형의 응력 또는 변형을 가해서 나타나는 에너지의 손실과 변형에서 회복되는 탄성의 정도를 구하는 것이다. 어떤 주기성을 갖는 변형을 가해서, 응력의 변화를 진동수(ω)의 함수로 측정하여 유변학적 성질을 나타내는 방법이다.
자, 어떤 샘플에 힘을 가하고, 힘에 대한 변형을 측정한다고 하자.
이때 재료에 진동수(주기의 역수)가 ω인 응력이 가해지면, 이에 대한 응답으로 변형이 발생될 것이다.
완전 탄성체인 경우에는 변형이 지연 없이(δ=0) 일어날 것이지만, 순수한 점성 액체의 경우에는 변형이 δ=π/2만큼 지연되어 발생할 것이다.
쉽게 말해서 무슨 의미이냐면, 위의 그림에서 완전 탄성체의 경우 G*에 기여하는 것은 G'밖에 없을 것이다. 따라서 그림에서 δ=0이 될 것이다. 그러나, 만약 순수 점성 액체하고 하면, G''만 기여하게 되고, δ=π/2 가 된다.
DMA에서는 진동수를 변화시키면서 나타나는 응력의 변화를 측정하고, 이때 변형이 얼마만큼 지연되어 나타나는지 측정하게 되고, 이로부터 G', G''을 구할 수 있다.
결과적으로는 G', G''로부터 손실 탄젠트(loss tangent)인 tanδ 를 구할 수 있고, 재료가 가지고 있는 상거동 특성을 이해할 수 있다.
예를 들어, 온도 또는 진동수를 변화시키며 응력의 변화를 측정하는데 손실 탄젠트가 작다는 것은 탄성이 우세하다는 것이고,
손실 탄젠트가 최대값을 가진다는 것은 위상 지연이 극대화 되었다는 것, 즉 점도가 우세해지고 있다는 의미로, 재료의 상이 변하고 있음을 나타내는 것이다.
도움이 되셨다면 공감 ❤️ 댓글 💬 부탁드려요 💖
[참고 자료]
1. https://www.rheologylab.com/videos/storage-and-loss-modulus-for-beginners/
Storage modulus (G’) and loss modulus (G”) for beginners - Rheology Lab
Ever struggled with an intuitive definition of storage and loss modulus? Watch this video to learn the important bits of rheology super quick!
www.rheologylab.com
2. 김재광, 위정재 / DMA를 이용한 최신 고분자 소재의 분석 / 2018 / 고분자 과학과 기술
3. 송형용, 현규 / 유변물성을 이용한 고분자 물질의 분석 / 2017 / 고분자 과학과 기술
댓글